勾配降下法(理論編)
前回:最小二乗法(理論編)ではデータに対してそれっぽい直線を引くことを考えました。そのために誤差が最小になるような直線のパラメータ(a,b)を推定する問題を解きました。
今回はそのパラメータを推定する手段(プロセス)として「勾配降下法」を解説していきます。
記事を読まれている方の中には「パラメータ(a,b)の推定ならば前回すでにやったのでは?」と疑問に思う方がいるかもしれません。
確かに最小二乗法(実装編)でもパラメータの推定まで行い、それっぽい直線を引くところまで行いました。
しかし、今回扱うパラメータ推定の手段はより一般化されています。
言い換えれば、データに対して直線以外の線を引いた場合も同じ仕組みでパラメータの推定を行えるようにしたいのです。
データ分析をするにあたって、入手したデータがどのような線に沿って変動するかは定かではありません。そのため、変わり者な曲線にフィッティングする必要も出てくるでしょう。
そういった場面で登場するのが勾配降下法なのです。
勾配降下法
まずは前回と同じように「データにそれっぽい直線を引く問題」を扱って勾配降下法を理解していきます。

データと直線との誤差は図の青いお椀型で示すことができます。そして、目指すのはお椀型の底を示すパラメータ(a,b)です。
「最小二乗法」の記事で紹介した手法はaとbそれぞれについて数学的アイデアを駆使し、完全に答えが定まるまで直線の図示ができませんでした。
それに対し勾配降下法はどこか適当な位置に初期パラメータを置いてしまうのです。
この時点ではまったく「それっぽい直線」とは言えないものの、直線を引き、データ点との誤差が大きいかどうか評価を下すことはできそうです。
そして、そのパラメータが誤差を最小にしてくれているのかチェックしながらお椀型の底にだんだんと近付けていく手法なのです。
このように推定する過程で推定値がまるで坂道を下って行くかのように見えることから「勾配降下法」と名付けられています。
具体的な計算方法は以下の図を見てみましょう↓
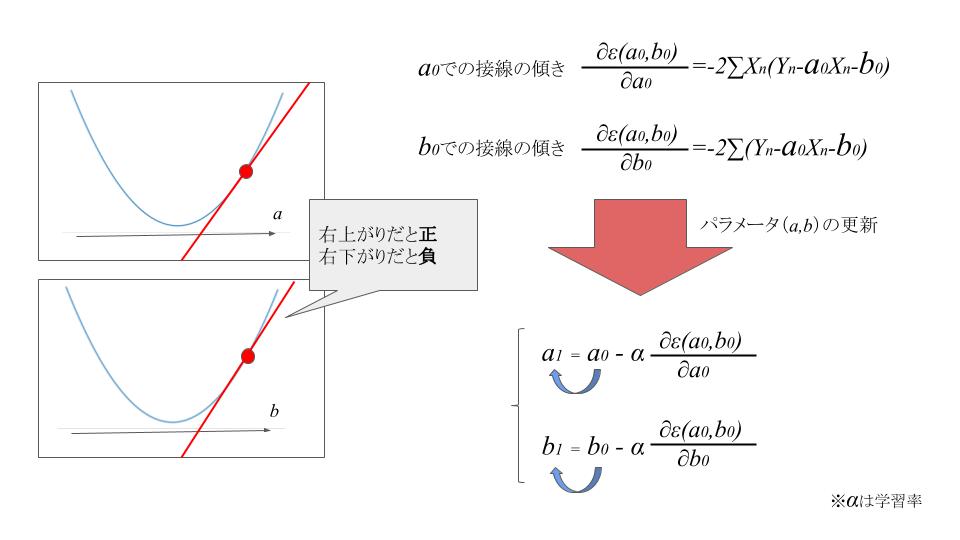
初期パラメータ(a,b)について確認します。
a0の値が中心点の右側にある場合は、値が本来求めたい数値よりも大きかったということになります。よって中心点に近づけるために何かしら値を引く必要がありそうです。
逆に、a0が中心点の左側にある場合は、値が本来求めたい数値よりも小さかったということになるため、何かしらの値を足す必要がありそうです。
では、どのような値を加えてやれば良いかというと、(a0,b0)それぞれにおける接線の傾きです。
初期パラメータ(a0,b0)それぞれについて誤差関数に偏微分を行い、接戦の傾きを導出します。
a0での接戦の傾き→∂ε(a0,b0)/∂a0
b0での接戦の傾き→∂ε(a0,b0)/∂b0
(※画像内の右上に書いてある式と同じ)
a0が中心点(お椀型の底)の右側にあるときは接戦の傾きは正の数になり、
a0が中心点(お椀型の底)の左側にあるときは接戦の傾きは負の数になります。
b0についてもまったく同じことがいえます。
接線の傾きをそのままパラメータ(a0,b0)に加えると求めたいお椀型の底に反した方向へ移動してしまうため、符号を変えて加えます。
(※図の右下参照)
a1 = a0 - ∂ε(a0,b0)/∂a0
b1 = b0 - ∂ε(a0,b0)/∂b0
また、学習の効率を上げるために学習率αをかけてからa0に足すこともあります。
(※学習率αはパラメータa0とはまったく違う意味を持った数値なので切り離して考えてください。)
a1 = a0 - α × ∂ε(a0,b0)/∂a0
b1 = b0 -α × ∂ε(a0,b0)/∂b0
この接線の傾きですが、中心点に近づけば近づくほど値が収束していきます。
つまり、真に求めたい値に近づけば近づくほど学習によって値が変化しなくなるということです。これは非常に都合の良いことです。
偏微分の手順を簡単にまとめると以下のようになります。
勾配降下法は導関数(誤差関数を偏微分したもの)どうしの連立方程式が1つに定められない場合も利用することができます。
ただし、極値(お椀型の底)を2つ以上もつ関数に対しては本来求めるべきパラメータ以外の場所で収束する可能性があります。